Arithmetic Operations on Complex Numbers
Addition of two complex numbers ![]() and
and ![]() is carried out thus:
is carried out thus:
![]()
![]()
![]() .
.
The real part of ![]() is therefore
is therefore ![]() and the imaginary part is
and the imaginary part is ![]() .
.
In a similar way,
![]()
![]()
![]() .
.
The real part of ![]() is therefore
is therefore ![]() and the imaginary part
and the imaginary part ![]() .
.
If ![]() and
and ![]() what is
what is
i) ![]()
ii)![]()
Solutions:
i) ![]() .
.
ii) ![]() .
.
Multiplication of two complex numbers ![]() and
and ![]() is carried out thus:
is carried out thus:
![]() .
.
The real part of ![]() is therefore
is therefore ![]() and the imaginary part is
and the imaginary part is ![]() .
.
If ![]() and
and ![]() what is
what is
i) ![]()
ii)![]()
Solutions:
i)
![]()
![]() .
.
ii)
![]() .
.
Division is achieved through use of the complex congugate, ![]() , i.e.
, i.e. ![]() with the sign of the imaginary part reversed. It will be noted that
with the sign of the imaginary part reversed. It will be noted that
![]() i.e. a real, positive number.
i.e. a real, positive number.
Division of a complex number ![]() by another complex number
by another complex number ![]() is facilitated by multiplying both numerator and denominator by
is facilitated by multiplying both numerator and denominator by ![]() giving
giving
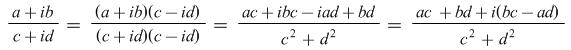 .
.
Convert the fraction ![]() to the form
to the form ![]() .
.
Solution:
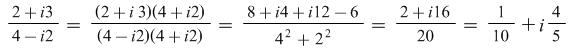 .
.
Powers of pure imaginary numbers of the form ![]() are found by calculating
are found by calculating ![]() and
and ![]() separately and multiplying the two results together.
separately and multiplying the two results together.
Calculate ![]() where
where ![]() .
.
Solution:
![]() .
. ![]() .
.
![]() .
.
Therefore,
![]() .
.
Powers of complex numbers of the form ![]() can be calculated by expanding
can be calculated by expanding ![]() . However, for large values of
. However, for large values of ![]() this calculation may be tedious, or, indeed, impractical.
this calculation may be tedious, or, indeed, impractical.
An easier method is to use de Moivre's formula
![]() .
.
Calculate ![]() where
where ![]() .
.
Solution:
The modulus of ![]() is found by
is found by ![]() .
.
The argument of ![]() is found by
is found by ![]() (noting that
(noting that ![]() is in the first quadrant).
is in the first quadrant).
![]() can therefore be re-written as
can therefore be re-written as
![]()
Using de Moivre's formula,
![]()
![]() .
.
Roots of complex numbers are also found using de Moivre's formula, this time in the form
![]() .
.
When dealing with real numbers, we are used to there being a maximum of two solutions when calculating roots i.e. two solutions, ![]() , for even roots, and one solution,
, for even roots, and one solution, ![]() , for odd roots. However, when calculating complex roots, there are
, for odd roots. However, when calculating complex roots, there are ![]() different solutions for
different solutions for ![]() roots.
roots.
i) Find the complex 4th roots of ![]() .
.
ii) Find the complex 3rd (cube) roots of ![]() .
.
i) Solution:
The modulus of ![]() is clearly given by
is clearly given by ![]() . The argument of
. The argument of ![]() is zero, since
is zero, since ![]() lies on the positive real axis. The complex 4th roots of
lies on the positive real axis. The complex 4th roots of ![]() are therefore given by
are therefore given by
![]()
i.e. the roots are ![]() . The results can easily be verified by calculation.
. The results can easily be verified by calculation.
ii) Solution: The modulus of ![]() is given by
is given by ![]() .
.
The argument of ![]() is
is ![]() , since
, since ![]() lies in the 2nd quadrant of the Argand diagram.
lies in the 2nd quadrant of the Argand diagram.
The complex cube roots of ![]() are therefore given by
are therefore given by
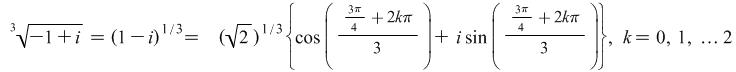
![]()
![]()